Terme und Ausdrücke - Syntax

Zeichenreihen

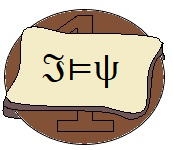
Zunächst definieren wir uns eine Menge, genannt das Alphabet, $\Sigma$ , die alle Symbole enthält, mit denen wir von nun an arbeiten wollen. ${\Sigma }^{\mathrm{*}}$ bezeichne die Menge der Wörter / Zeichenreihen über Σ, auch kleenesche Hülle genannt.

Beispiel

Haben wir die Menge $\Sigma =\{h,a,l,o\}$ , so sind ein paar Elemente von ${\Sigma }^{\mathrm{*}}\text{:} \mathrm{hallo},\mathrm{hola},\mathrm{lola},\mathrm{...}$ (Beachte, dass alles klein Geschrieben ist, weil Großbuchstaben $\notin \Sigma$ ). Aber auch hhhhhhhhhhhhh, hoooolhhh, aoooooh sind in ${\Sigma }^{\mathrm{*}}$ enthalten. Sei $\Sigma$ nun $\{\int ,x,d,+,1,(,\left)\right\}$ . Dann ergibt sich: $\int x+1dx,\int (x+1)dx$ (Für die Spießer.) $,\int dx(x+1)$ (Für die Quantenfetischisten.). Natürlich haben wir aber auch hier wieder ungebetene Gäste: $x(\int 1,\left)\right(,1x$ (Widerwertig! Da kann man auch $x$ schreiben! >:-( ).
Wörter sind also endliche Verkettungen der Elemente von $\Sigma .$ Um diesem Problem, der sinnlosen Zeichenreihen zu entgehen, führen wir sogenannte Kalküle ein.

Kalküle

Kalküle sind Regeln, die es uns erlauben, gewisse Zeichenreihen aus unserer Symbolmenge $\Sigma$ abzuleiten. In der Regel werden sie in der Form $\frac{{\zeta }_0,{\zeta }_1,\mathrm{...},{\zeta }_{\mathrm{n}}}{\zeta }$ notiert. Aber was bringt uns der Schwachsinn jetzt?! Sowohl ${\zeta }_0,{\zeta }_1,\mathrm{...},{\zeta }_{\mathrm{n}}, \text{als auch} \zeta$ sind Zeichenreihen über unserer Symbolmenge. Dieser Bruch sagt uns nun: Sind ${\zeta }_0,{\zeta }_1,\mathrm{...},{\zeta }_{\mathrm{n}}$ von uns gewollte Zeichenreihen, so ist $\zeta$ eine von uns gewollte Zeichenreihe. Wie, das war jetzt nicht verständlich???

Beispiel

Also gut, du Diva. Angenommen wir haben die Symbolmenge $\Sigma =\{1,2,3,4,5,6,7,8,9,+\}$ . Gültige Zeichenreihen sollen jetzt die natürlichen Zahlen (die keine 0 enthalten) sein oder Summen von je zwei natürlichen Zahlen. Ich lasse 0 weg, weil 0 einige Dinge für einen ersten Kalkül verkomplizieren würden. Aber alles zu seiner Zeit. Wie sieht der Kalkül aus? Zunächst sind die einstelligen natürlichen Zahlen (ohne die 0), nennen wir sie ganz unkonventionell $n$ , gültige Zeichenreihen (Ja, eigentlich sind es bei einstelligen Zahlen keine Reihen, aber wer Modelltheoretiker ist, der ist so durch, dass ihn so etwas nicht mehr interessiert und er sagt: DAS IST SEHR WOHL EINE ZEICHENREIHE! ES GENÜGT DER DEFINITION!!!). Das beschreiben wir in unserer Notation mit $\frac{ }{n}$ . Prämissenlose Zeichenreichen beschreiben wir in unserer Notation also einfach, indem wir die obere Seite nicht auffüllen. Logisch (super Wortwitz), wir können diese Zeichenreihen aus keinen anderen herleiten, sie sind ja prämissenlos. Jetzt sind aber auch mehrstellige Zahlen im Sinne unseres, oder eher meines, Willens gültige Zeichenreihen. Das beschreiben wir mit $\frac{n_0,n_1,\mathrm{...},n_{\mathrm{i}}}{m}$ . Was heißt das jetzt? Im Grunde ganz einfach (Das sagen sie immer...): $n_0,n_1,\mathrm{...},n_{\mathrm{i}}$ sind einstellige Zahlen, haben wir eine beliebige (Endliche!) Anzahl an einstelligen Zahlen, welche gültig nach unserem bisherigen Kalkül (das ja nur aus einer Regel besteht) sind, so ist auch die Zahl, welche sich aus diesen zusammensetzt eine gültige Zeichenreihe. Ganz konkret: Nach unserer bisherigen Regel sind nur 1, 2, 3, 4, 5, 6, 7, 8 und 9 gültige Zeichenreihen. Mit unserer neuen Regel ist jetzt aber auch, zum Beispiel, 42 eine gültige Zeichenreihe, da 2 eine gültige Zeichenreihe ist und 4 ebenfalls, aber auch 7331, da 7, 3 und 1 gültige Zeichenreihen sind. 404 hingegen ist keine gültige Zeichenreihe, da sie eine 0 enthält. Für das große Finale, die Addition von zwei Zahlen, finden wir $\frac{m_1,m_2}{m_1+m_2}$ . Um die Bedeutung dieses Kalküles zu analysieren, fassen wir noch einmal alle Regeln zusammen: Mit 1. sehen wir, dass jede einstellige Zahl (außer 0) eine gültige Zeichenreihe ist. Aus 2. können wir das ebenfalls ableiten, denn geben wir bei 2. oben nur eine Zahl herein, erhalten wir unten die gleiche Zahl. Gleichzeitig sind nach 2. mehrstellige Zahlen (die keine 0 enthalten) Zeichenreihen. Mit 3. sind mit allen Zeichenreihen, die aus 2. ableitbar sind auch die Summen jeweils zweier gültiger Zeichenreihen nach unserer Festlegung gültige Zeichenreihen.

Beispiel

Behauptung: Nach unserem Kalkül ist 451 + 3 eine gültige Zeichenreihe.

Beweis: Nach 1. ist 3 eine gült. Zr.. Nach 2. ist 3 eine gült. Zr., da 3 nach 1. eine gült. Zr. ist. Da 3 nach 2. eine gült. Zr. ist, dürfen wir 3 für 3. verwenden. 451 ist nach 2. eine gült. Zr., da 4, 5 und 1 nach 1. gült. Zr. sind. Also dürfen wir 451 für 3. verwenden. Da 3 und 451 nach 2. gült. Zr. sind, ist 3 + 451 nach 3. eine gült. Zr..
q. e. d.

Terme

So, jetzt geht es ans Eingemachte. Rekapitulieren wir kurz, was Terme sind. In der Schule lernte man, dass Terme sinnvolle Rechenausdrücke sind, die aus Zahlen, Variablen, Rechenzeichen und Klammern bestehen (Also, z.B., Zeichenreihen der Form $5x(2+x)$ ); aber wie so vieles, was man in der Schule lernt, ist das nur halbgar und sehr, sehr ungenau. Wir formalisieren, was wir unter einem Term verstehen und geben mithilfe von Kalkülen eine exakte Definition an. In diesem Abschnitt führen wir auch das Beweisprinzip der Induktion in Kalkülen ein, etwas, das wir im Grunde gerade schon getan haben.
Aber bevor wir das angehen, führen wir ein paar Konventionen ein. Von nun an bezeichnet unser Alphabet 𝒜 folgende Menge:

1. Variablen $v_0,v_1,v_2,...$
2. logischen Junktoren $\neg ,\vee ,\wedge ,\to ,\leftrightarrow$
3. Quantoren $\exists ,\forall$
4. Klammern $),($
5. Gleichheitszeichen (eigentlich Identischzeichen) $\equiv$ (Wir besprechen noch, warum wir plötzlich diese Erscheinung wählen.)

Hinzu tritt die Menge S, sie enthält:

1. eine (eventuell leere) Menge von Konstantensymbolen: $c_0,c_1,c_2,...$

$\forall n\ge 1$ :

2. eine eventuell leere Menge von (untereinander verschiedenen!) n-stelligen Funktionssymbolen: ${f_0}^n,{f_1}^n,{f_2}^n,...$
3. eine (eventuell leere) Menge von (untereinander verschiedenen!) n-stelligen Relationssymbolen: ${R_0}^n,{R_1}^n,{R_2}^n,...$

S nennen wir von nun an die Symbolmenge und ${\Sigma }_S:=\Sigma \bigcup S$ ist das Alphabet unserer Sprache $L^S$ (Σ ist zwar auch ein Alphabet, aber nicht das für die Sprache spezifische Alphabet). Wie haben wir Funktionen und Relationen zu verstehen? Es ist im Grunde recht einfach, die Funktionen, die wir hier behandeln sind Abbildungen $f:D^n\to D$ (kartesisches Produkt), also von geordneten Paaren einer Menge auf ein Element der Menge, ebenso sind unsere Relationen Teilmengen von D. Jetzt kommen wir aber endlich zur Definition von Termen.

Definition

$S\text{-Terme}$ sind diejenigen Wörter über ${{\Sigma }_S}^{*}$ , welche man durch eine endlichmalige Anwendung folgender Regeln erhalten kann:

1. Jede Variable ist ein $S\text{-Term}$ .
2. Jede Konstante aus $S$ ist ein $S\text{-Term}$ .
3. Sind die Zeichenreichen $t_0,...,t_{\mathrm{n}} S\text{-Terme}$ und ist $f$ ein $n\text{-stelliges}$ Funktionssymbol aus $S$ , so ist $f{t}_0,...,t_{\mathrm{n}}$ ein $S\text{-Term}$ .

Formalisiert: Wie können wir daraus jetzt konkret Terme basteln? Dazu müssen wir verstehen, dass Addition, Subtraktion, Multiplikation und Division im Grunde Abbildungen $+:{ℝ}^2\to ℝ$ sind. Abbildungen können wir komponieren und damit können wir die Klammern ersetzen. Unseren Term $5x(2+x)$ können wir in der Funktionsschreibweise als $\times (\times (5,x),+(2,x\left)\right)$ ausdrücken. Wir sehen, zuerst werden die Funktionswerte des + und des inneren × bestimmt, danach die, des äußeren ×; die Position der +-Funktion ersetzt also die Rolle der Klammern. Wir nehmen also auch mit: Verknüpfungen sind Abbildungen und ihre Verschaltung, ihre Komposition, entscheidet, was wir zuerst berechnen. Die Komposition nimmt also den Platz ein, den bisher die Klammern innehatten.

Ausdrücke / Formeln

$2+2=4$ , $5>2$ und $f\left(x\right)=0$ sind Beispiele für mathematische Ausdrücke, die uns allen geläufig sein sollten, wenn das nicht der Fall ist, warst du im Matheunterricht wohl Kreide holen. Auch unter Formeln sollte sich jeder etwas Vorstellen können, zum Beispiel: $a^2+b^2=c^2,x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a},T=2\pi \sqrt{\frac{k}{m}}$ oder auch $iħ\frac{\partial \Psi (r,t)}{\partial t}=(-\frac{{ħ}^2}{2m}\Delta +V(r,t\left)\right)\Psi (r,t)$ . Wir wollen den Begriff des Ausdrucks, bzw. der Formel, formalisieren.

Definition

$S\text{-Ausdrücke}$ sind diejenigen Wörter über ${{\Sigma }_S}^{*}$ , welche man durch eine endlichmalige Anwendung folgender Regeln erhalten kann:

1. Sind $t_0,t_1\hspace{0.17em}S\text{-Terme}$ , so ist $t_0\equiv t_1$ ein $S\text{-Ausdruck}$ .
2. Sind $t_0,...,t_{\mathrm{n}} S\text{-Terme}$ und ist $R$ ein $n\text{-stelliges}$ Relationssymbol aus $S$ , so ist $R{t}_0,...,t_{\mathrm{n}}$ ein $S\text{-Ausdruck}$ .
Ausdrücke, die mit 1. oder 2. gewonnen werden können, heißen atomar, da sie nicht aus anderen Ausrücken zusammengesetzt sind.
3. Ist $\phi$ ein $S\text{-Ausdruck}$ , so ist $\neg \phi$ ebenfalls ein $S\text{-Ausdruck}$ .
4. Sind $\phi ,\psi \hspace{0.17em}S\text{-Ausdrücke}$ , so sind $(\phi \vee \psi ),(\phi \wedge \psi ),(\phi \to \psi )$ und $(\phi \leftrightarrow \psi )$ ebenfalls $S\text{-Ausdrücke}$ .
5. Ist $x$ ein eine Variable und $\phi$ ein $S\text{-Ausdruck}$ , so sind $(\exists x\phi )$ und $(\forall x\phi )$ ebenfalls $S\text{-Ausdrücke}$ .

Formalisiert: Unsere Sprache $L^S ist\; die\; Menge\; aller,\; nach\; den\; gerade\; genannten\; Regeln\; gebauten,\; Ausdrücke.$