Die Axiome der Zermelo-Fraenkel-Mengenlehre

Eine Menge ist eine Ansammlung von Objekten. Diese Definition einer Menge ist bestimmt die erste, mit der jeder von uns das mathematische Konzept einer Menge kennengelernt hat. Doch diese naive Definition bringt einige Probleme mit sich. Das bekannteste dürfte die sogenannte Russellsche Antinomie sein.

Die Menge aller Mengen, die sich nicht selbst enthalten.

Enthält sich diese Menge selbst, wenn ja, dann tut sie es nicht, wenn sie sich nicht enthält, dann tut sie es; ein Bilderbuchparadoxon. Wir müssen das mathematische Konzept einer Menge überdenken, es sei denn, wir wollen eine Mathematik voller Paradoxa. Was wir tun müssen, ist die Mengenlehre auf eine axiomatische Basis stellen; genau das tun wir mit dem ZFC, dem Zermelo-Fraenkel-Axiomensystem mit dem Auswahlaxiom (Bitte lyncht mich nicht, weil ich das Auswahlaxiom verwende.). Im Folgenden gehen wir die Axiome durch, um am Ende die Redundanz dieses Axiomensystems zu behandeln und zu diskutieren, welche Axiome wir fortlassen können.

Das Existenzaxiom (EX)

$\exists x(x=x)$
Es existiert eine Menge. Trivial.

Das Extensionalitätsaxiom (EXT)

$\forall x\left(\forall y\right(\left(\forall z\right((z\in x)\leftrightarrow (z\in y)\left)\right)\to (x=y)\left)\right)$
Mengen, welche die gleichen Elemente beinhalten, sind gleich.

Das Schema der Aussonderungsaxiome (AUS)

$\forall p_0,...,p_n\left(\forall x\right(\exists y\left(\forall z\right((z\in y)\leftrightarrow$ $\left(\right(z\in ;x)\wedge \phi (p_0,...,p_n,z\left)\right)\left)\right)\left)\right)$
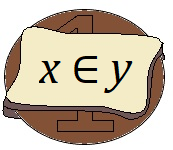
Für alle Mengen $p_0,...,p_n$ und $x$ gibt es eine Menge, welche genau diejenigen Elemente von $x$ enthält, für die die Beziehung $\phi (p_0,...,p_n,z)$ gilt.